4-9-2001

O valor de p

A primeira referência ao valor de p (pi) aparece na Bíblia, no Primeiro Livro dos Reis, 7, versículo 23: “Fez mais o mar de fundição, de dez côvados, de uma borda até à outra borda, redondo ao redor, e de cinco côvados ao alto; e um cordão de trinta côvados o cingia, em redor.”  Aqui, o valor de p é 3, bastante inexacto, portanto.

Desde sempre, este número mágico despertou a atenção dos estudiosos. Os historiadores calculam que, desde 2000 a.C., os homens têm consciência de que a razão entre a circunferência e o seu diâmetro é igual para todos os círculos. Deram conta que, se duplicarem a distância através de um círculo, então também a distância em volta dele é igual ao dobro. Em notação algébrica, diremos que

em que o valor de p é constante. Note-se que o nome “pi”, usando a letra grega, só foi introduzido em 1706 por William Jones (1675-1749).

 O valor exacto de p desde cedo despertou o interesse dos matemáticos. Arquimedes de Siracusa (287-212 a.C.)   chegou ao valor de 22/7 ou seja 3,142857…

 Só no sec. XVIII é que se provou que p é um número irracional, isto é que não pode ser expresso como uma fracção, própria ou imprópria. Em termos  práticos, isso significa que o número de casas decimais que p pode ter é infinito.

 No sec. XIX, demonstrou-se que p é um número transcendental, isto é, não pode ser expresso por uma equação algébrica com coeficientes racionais.

 Como corolário, deve dizer-se que é impossível fazer a “quadratura do círculo”, isto é, desenhar um quadrado com  o mesmo perímetro de determinado círculo.

 Podem apreciar-se na tabela a seguir os progressos feitos no cálculo do valor de p.  Só no sec. XX., nos anos 50, é que se começaram a utilizar computadores para o cálculo das casas decimais de p.

 Os valores de p através dos séculos

O valor de p com 10 000 casas decimais pode ser visto aqui. Hoje é possível calculá-lo com mais de dez mil milhões de casas decimais (para quê?)

Eis algumas das fórmulas utilizadas para calcular o valor de p em computador:

François Viète (1540-1603) determinou que:

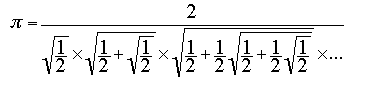
John Wallis (1616-1703) mostrou que:

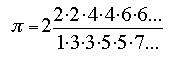
Euler (1707-1783) construiu esta fórmula:

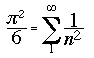
Para conseguir decorar valores longos de p, começaram a ser inventadas mnemónicas, como esta, com 23 casas decimais, em que o número das letras de cada palavra representa um algarismo:

 How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics. All of thy geometry, Herr Planck, is fairly hard...:

3.14159265358979323846264...

 Sites sobre o p:

Notícias sobre o mundo do Pi

Directório de J.M.Borwein

A history of Pi

Squaring the circle

Finding the value of Pi

Pi Land of Eve Astrid Andersson

NOTAS:

 1 - Abu Ja'far Muhammad ibn Musa Al-Khwarizmi (ver também o excelente site de Roberto Lyra), matemático árabe nascido em Bagdad, por volta de 780, faleceu em 850. Do seu nome derivam as palavras "algarismo" em português e "guarismo" em castelhano (guardámos sempre o artigo árabe nas palavras derivadas daquela língua).  Para além disso, escreveu um livro chamado "al-Kitab al-mukhtasar fi hisab al-jabr wa'l-muqabala" (traduzido para inglês com o título "The Compendious Book on Calculation by Completion and Balancing”. De Al jabr, vem o nome Álgebra. Mais: sabe-se que Al-Khwarizmi escreveu um livro que desapareceu, mas de que chegou até nós uma tradução latina com o título "Algoritmi de numero Indorum", ou seja, "Al-Khwarizmi sobre o modo Hindu de contar" e do nome latino que ali lhe deram derivou o termo "algoritmo".

2 – Um número irracional é aquele que não pode ser expresso como uma fracção (própria ou imprópria). Fracção própria é a que tem o numerador inferior ao denominador. Fracção imprópria é aquela em que o numerador é maior ou igual ao denominador. O  numerador e o denominador são, evidentemente, inteiros. Um número primo é um número maior do que 1, que não é divisível por nenhum número inteiro positivo, que não seja 1 ou o próprio número. Um número composto é um número inteiro positivo diferente de 1 e que não é número primo.

3 – Os números transcendentais não podem ser expressos como sendo a raiz de uma qualquer equação algébrica, com coeficientes racionais. Isto significa  que p não pode satisfazer com exactidão equações do tipo p² = 10, 9 p⁴- 240 p² + 1492 = 0. Este tipo de equações envolve sempre números inteiros para o valor de p. O número p pode ser expresso através de uma fracção que não tem fim ou como o limite de uma série infinita. A fracção 355/113 exprime o valor de p com exactidão até seis casas decimais.

Em 1882, o matemático alemão F. Lindemann provou que p é transcendental, acabando com 2 500 anos de especulação. Com efeito, provou que p transcende o poder de a álgebra o representar na sua totalidade. Não pode ser representado através de qualquer série finita de operações aritméticas ou algébricas. Não pode ser escrito num pedaço de papel tão grande como o universo.